Syllabus for 5 Years Integrated M.Sc.(Mathematics)
  1. Home
  2. Programmes
  3. Syllabus for 5 Years Integrated M.Sc.(Mathematics)
5 Years Integrated M.Sc.(Mathematics)
Course Details
Eligibility Criteria
12th passed in Science stream with group A or AB.
Intake

60 Seats

Duration

The duration of the course shall be full time 5 - years Integrated academic years (i.e. 10 semesters)

Curriculum
Please visit the link below
View Syllabus
SEMESTER - 1   Teaching Evaluation Scheme
Code Subjects
060090101 AECC1 Professional Commnunications
060090105 CC1 Differential and Integral Calculus
060090106 CC2 ElementaryAlgebra
060090107 GE1 Principles of Scientific Computing
SEMESTER - 2
2016 - 17   Teaching Evaluation Scheme
Code Subjects
060090201 AECC2 Environmental Studies
060090205 CC3 Advanced Calculus
060090206 CC4 Linear Algebra
060090207 GE2 Mathematical Finance
OLD
Code Subjects
060090201 AECC2 Environmental Studies
060090202 CC3 Real analysis
060090203 CC4 Differential equations
060090204 GE2 Econometrics
SEMESTER - 3
2017 - 18   Teaching Evaluation Scheme
Code Subjects
060090308 CC5 Real Analysis
060090309 CC6 Ordinary Differential Equations
060090303 CC7 Fundamentals of Numerical Analysis
Elective Subjects:
Students will opt only one from SEC1 and one from GE3 therefore only 08 credits have been added in total credits.
060090304 SEC1 Mathematical Logic and Function
060090305 SEC1 Business Mathematics
060090306 GE3 Basics of Statistics
060090307 GE3 Biomathematics
2016 - 17
Code Subjects
060090301 CC5 Advanced Calculus
060090302 CC6 Linear Algebra
060090303 CC7 Fundamentals of Numerical Analysis
060090304 SEC1 Mathematical Logic and Function
060090305 SEC2 Business Mathematics
060090306 GE3 Basiscs of Statistics
060090307 GE4 Biomathematics
SEMESTER - 4
2016 - 17   Teaching Evaluation Scheme
Code Subjects
060090401 CC8 Advanced Real Analysis
060090402 CC9 Higher Order Differential Equations and Transforms
060090403 CC10 Numerical Analysis
Elective Subjects:
Students will opt only one from SEC2 and one from GE4 therefore only 08 credits have been added in total credits.
060090404 SEC2 Combinatorial Mathematics
060090405 SEC2 Industrial Mathematics
060090406 GE4 Statistical Analysis
060090407 GE4 Application of Algebra
SEMESTER - 5
2017 - 18   Teaching Evaluation Scheme
Code Subjects
060090501 CC11 Complex Analysis
060090502 CC12 Integral Transforms
060090507 AECC3 Soft Skills and Career Development
Elective Subjects:
Students will opt only one from DSE1 and one from DSE2 therefore only 12 credits have been added in total credits.
060090503 DSE1 Discrete Mathematics and Graph Theory
060090504 DSE1 Differential Geometry
060090505 DSE2 Group Theory
060090506 DSE2 Fundamentals of Classical Mechanics
SEMESTER - 6
2018 - 19
Code Subjects
060090601 CC13 Partial Differential Equations
060090602 CC14 Mathematical Modelling
Elective Subjects:
Students will opt only one from DSE3and one from DSE4 therefore only 12 credits have been added in total credits.
060090603 DSE3 Number Theory
060090604 DSE3 Control Theory
060090605 DSE4 Ring and Field Theory
060090606 DSE4 Theory of Equations
SEMESTER - 7
2018 - 19
Code Subjects
060090701 CC15 Topology
060090702 CC16 Functional Analysis
060090703 CC17 Advanced Numerical Analysis
060090704 CC18 Advance Partial Differential Equations
060090705 DSE 5 Fuzzy Logic
Fee Structure
1. Tuition Fee

Rs. 15,000 Per Semester (UG)

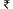
Rs. 25,000 Per Semester (PG)

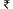
Per Semester* (Applicable as per fee regulatory committee appointed by Government of Gujarat)

2. Other Fee

3,250 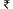Per Semester

(It includes Cultural Activities, Sports Activities, Internal Examination, Laboratory support, Books support, Student Welfare, Campus Development)

3. One Time Fee

6,150 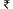At time of admission
(It includes College Deposit, Registration, and I-Card)

Programme Outcome (PO) & Programme Specific Outcomes (PSO)
Programme Outcome (PO)
  • PO 1: Knowledge: Provides knowledge about the fundamentals of pure, applied and computing mathematics and its applications to students that creates the opportunitiesin industries and research centers.
  • PO 2: Core Competence: Creates competency in science and mathematics to formulate, analyses and solve problem and/or also to pursue advanced study or research.
  • PO 3:Breadth: Trainsstudents having good knowledge in unearth core of academia and industry by the roots of mathematics.
  • PO 4: Evaluation: Imparts in students to raise trial and error based curiosity and problem solving functionality with research based advanced tutorial for higher level decision makings tools.
Programme Specific Outcomes (PSO)
  • PSO-1:Understand thefundamental principles underlying the major areas of mathematics.
  • PSO-2: Evaluatealogical, reasoning andmathematics savvy approach.
  • PSO-3: Explorea newer way of mathematical applications.
  • PSO-4: Create an attribute towards problem solving and research orientation.
  • PSO-5: Able to apply analytical and theoretical skills to model and solve mathematical problems.
  • PSO-6: Develop mathematical computing skills to solve complex mathematical models.
Trasportation
Libraries
Hostels
Sports